[알고리즘] C++ 여러가지 자료형 (feat. 바킹독)

정수 자료형

char 자료형은 1byte = 8 bit 이다.

 

unsigned char 자료형의 범위: 0 ~ \(2^{0}\) +  \(2^{1}\) + ··· + \(2^{7}\) (= \(2^{8}\) - 1 = 255)

 

char 자료형의 범위:  -\(2^{7}\)(= -128) ~ \(2^{0}\) + \(2^{1}\) + ··· + \(2^{6}\) (= \(2^{7}\) - 1 = 127)

 

short(2 byte): \(2^{15}\) - 1 (= 32767)

int(4 byte):  \(2^{31}\) - 1 (21억)

long long(8 byte):  \(2^{63}\) - 1

 

* int가 long long보다 연산 속도와 메모리 모두 우수하지만 int 자료형이 표현할 수 있는 범위를 넘어서는 수를 저장해야 한다면 반드시 long long 자료형을 사용해야 한다.

 

Integer Overflow

컴퓨터는 명령받은 대로 이진수 계산을 하기 때문에 이런 현상이 발생한다.

 

example)

// 128번에 걸쳐 hi를 출력하는 함수
void func1() {
	for(char s=0; s<128; s++) {
    	cout << "hi";
    }
}

s가 127이 된 후에 1이 더해질 때 -128이 되어 무한루프에 빠지게 된다.

해결방법: s의 자료형을 char에서 int로 바꾼다.

 

//10의 10 거듭제곱을 1000000007로 나눈 나머지를 반환하는 함수
int func3() {
    int a = 10;
    int mod = 1000000007;
    for (int i = 0; i < 10; i++)
        a = 10 * a % mod;
    return a;
}

a 가 \(10^{9}\) 일 때 10이 곱해지는 순간 int의 최대 범위를 넘어서서 Integer Overflow 발생

해결방법: a의 자료형을 long long으로 바꾸거나 6번째 줄에서 10대신 10ll 혹은 (long long)10으로 강제 형변환

 

실수 자료형

float (4 byte)

double (8 byte)

 

실수를 나타낼 때 sign, exponent, fraction field로 나누어진다.

 

sign: 해당 수가 음수인지 양수인지 저장하는 필드

exponent: 과학적 표기법에서의 지수를 저장하는 필드

fraction: 유효숫자 부분을 저장하는 필드

 

실수 자료형을 이진수로 나타내는 방법

 

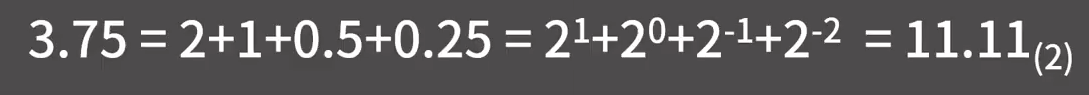
실수 자료형 주의할 점

1. 실수의 저장/연산 과정에서 반드시 오차가 발생할 수 밖에 없다.

2. double에 long long 범위의 정수를 함부로 담으면 안된다.

3. 실수를 비교할 때는 등호를 사용하면 안된다.

 

 

 

참고자료

https://www.youtube.com/watch?v=9MMKsrvRiw4